
Zadanie Podróż (pod)
Pomóż nam usprawnić bazę zadań!
Podróż
Limit pamięci: 32 MB
Rozważmy graf opisujący sieć komunikacji publicznej,
np. sieć autobusową, tramwajową, metra, itp.
Wierzchołki grafu, o numerach 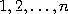 , reprezentują
przystanki, a krawędzie
, reprezentują
przystanki, a krawędzie 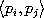 ,
(dla
,
(dla 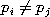 )
oznaczają możliwe, bezpośrednie przejazdy od przystanku
)
oznaczają możliwe, bezpośrednie przejazdy od przystanku 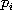 do
do
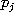 (
(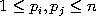 ).
).
W sieci kursują pojazdy linii komunikacyjnych.
Linie komunikacyjne oznaczone są numerami 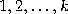 .
Linia komunikacyjna
.
Linia komunikacyjna 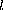 zdefiniowana jest przez ciąg przystanków
zdefiniowana jest przez ciąg przystanków
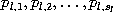 ,
przez które przejeżdżają pojazdy linii, oraz czasy
przejazdów
,
przez które przejeżdżają pojazdy linii, oraz czasy
przejazdów 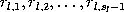 pomiędzy przystankami -
pomiędzy przystankami - 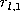 jest czasem przejazdu od przystanku
jest czasem przejazdu od przystanku
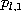 do
do 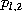 , lub z powrotem, tj. od przystanku
, lub z powrotem, tj. od przystanku
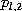 do
do 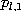 ;
;
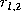 jest czasem przejazdu od przystanku
jest czasem przejazdu od przystanku 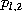 do
do 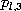 , itd.
Wszystkie przystanki linii są różne, tj. dla
, itd.
Wszystkie przystanki linii są różne, tj. dla 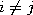 zachodzi
zachodzi
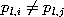 .
.
Na danej linii 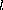 pojazdy kursują z określoną częstotliwością
pojazdy kursują z określoną częstotliwością
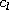 , gdzie
, gdzie 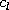 jest liczbą ze zbioru
jest liczbą ze zbioru 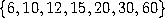 .
Pojazdy linii wyruszają z przystanku
.
Pojazdy linii wyruszają z przystanku 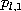 o każdej "okrągłej"
godzinie doby,
o każdej "okrągłej"
godzinie doby, 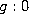 , (
, (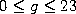 ),
a następnie zgodnie z częstotliwością linii, a więc o godzinach
),
a następnie zgodnie z częstotliwością linii, a więc o godzinach
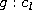 ,
, 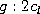 , ... itd.
(
, ... itd.
(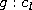 oznacza "
oznacza "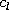 minut po godzinie
minut po godzinie 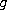 ").
Ruch pojazdów linii odbywa się jednocześnie w obu kierunkach:
z przystanku
").
Ruch pojazdów linii odbywa się jednocześnie w obu kierunkach:
z przystanku 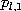 do
do 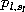 ,
a także z przystanku
,
a także z przystanku 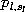 do
do 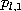 .
Godziny odjazdów pojazdów linii z przystanku
.
Godziny odjazdów pojazdów linii z przystanku 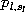 są takie same,
jak z przystanku
są takie same,
jak z przystanku 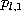 .
.
W tak zdefiniowanej sieci komunikacji publicznej chcemy odbyć podróż z
przystanku początkowego  ,
do przystanku końcowego
,
do przystanku końcowego 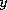 .
Zakładamy, że podróż
jest możliwa i
nie będzie trwała dłużej
niż 24 godziny.
W trakcie podróży możemy się przesiadać dowolną
liczbę razy z jednej linii komunikacyjnej na inną.
Przyjmujemy, że czas dokonania przesiadki jest równy 0, jednakowoż,
zmieniając linię musimy liczyć się z koniecznością
czekania na pojazd linii, do którego chcemy się przesiąść.
Naszym celem jest odbycie podróży z przystanku początkowego
.
Zakładamy, że podróż
jest możliwa i
nie będzie trwała dłużej
niż 24 godziny.
W trakcie podróży możemy się przesiadać dowolną
liczbę razy z jednej linii komunikacyjnej na inną.
Przyjmujemy, że czas dokonania przesiadki jest równy 0, jednakowoż,
zmieniając linię musimy liczyć się z koniecznością
czekania na pojazd linii, do którego chcemy się przesiąść.
Naszym celem jest odbycie podróży z przystanku początkowego  , do
przystanku końcowego
, do
przystanku końcowego 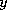 , w minimalnym czasie.
, w minimalnym czasie.
Przykład
Na poniższym rysunku przedstawiono schemat sieci komunikacyjnej o
6 przystankach i dwóch liniach: 1 i 2.
Pojazdy linii 1 kursują pomiędzy przystankami 1, 3, 4 i 6, a
linii 2 pomiędzy przystankami 2, 4, 3 i 5.
Częstotliwości kursowania pojazdów linii wynoszą, odpowiednio,
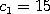 oraz
oraz 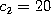 .
Czasy przejazdów pomiędzy przystankami umieszczono obok
krawędzi sieci opatrując je indeksami 1 i 2 dla poszczególnych linii.
.
Czasy przejazdów pomiędzy przystankami umieszczono obok
krawędzi sieci opatrując je indeksami 1 i 2 dla poszczególnych linii.
![[ rysunek do przykładu ]](images/OI8/podroz.gif)
Załóżmy, że o godzinie 23:30 znajdujemy się na przystanku początkowym 5 i chcemy odbyć podróż do przystanku końcowego 6. Wówczas musimy odczekać 10 minut i o godzinie 23:40 wyjeżdżamy linią 2. Nasza podróż może mieć dwa warianty. W pierwszym wariancie, po dojechaniu do przystanku 3 o godzinie 23:51 i odczekaniu 3 minut, przesiadamy się o godzinie 23:54 na linię 1 i dojeżdżamy do przystanku 6 o godzinie 0:16 (następnego dnia). W drugim wariancie, dojeżdżamy linią 2 do przystanku 4 o godzinie 0:8, czekamy 13 minut i o godzinie 0:21 wsiadamy do pojazdu linii 1, osiągając przystanek końcowy 6 o godzinie 0:31. Tak więc najwcześniej możemy dotrzeć do przystanku 6 o godzinie 0:16.
Zadanie
Napisz program, który:
-
wczyta ze standardowego wejścia opis sieci oraz linii
komunikacyjnych, numer przystanku początkowego
 ,
numer przystanku końcowego
,
numer przystanku końcowego 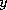 ,
godzinę początkową
,
godzinę początkową 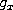 oraz minuty początkowe
oraz minuty początkowe 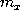 ,
,
-
wyznaczy minimalny czas podróży od przystanku
początkowego
 , do przystanku końcowego
, do przystanku końcowego 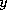 ,
,
-
wypisze na standardowe wyjście najwcześniejszą
możliwą godzinę z minutami dotarcia do przystanku
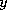 -
odpowiednio,
-
odpowiednio, 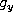 oraz
oraz 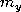 .
.
Wejście
W pierwszym wierszu standardowego wejścia zapisanych jest sześć liczb całkowitych, pooddzielanych pojedynczymi odstępami:
-
liczba przystanków
 (
(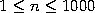 ),
),
-
liczba linii komunikacyjnych
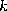 (
(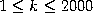 ),
),
-
numer przystanku początkowego
 (
(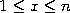 ),
),
-
numer przystanku końcowego
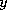 (
(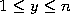 ),
),
-
godzina rozpoczęcia podróży
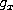 (
(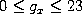 ),
),
-
minuta rozpoczęcia podróży
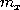 (
(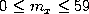 ).
).
 ,
a linie komunikacyjne od 1 do
,
a linie komunikacyjne od 1 do 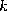 .
.
W kolejnych 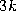 wierszach opisane są kolejne linie komunikacyjne -
opis każdej linii zajmuje trzy kolejne wiersze.
wierszach opisane są kolejne linie komunikacyjne -
opis każdej linii zajmuje trzy kolejne wiersze.
-
W pierwszym wierszu opisującym linię komunikacyjną
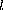 są
zapisane dwie liczby całkowite, oddzielone pojedynczym odstępem:
są
zapisane dwie liczby całkowite, oddzielone pojedynczym odstępem:
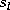 , równa liczbie przystanków
(
, równa liczbie przystanków
(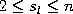 ), oraz
), oraz
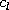 , równa częstotliwości kursowania pojazdów
(
, równa częstotliwości kursowania pojazdów
(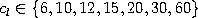 ).
).
-
W drugim wierszu opisującym linię komunikacyjną
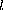 jest
zapisanych
jest
zapisanych 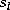 różnych liczb całkowitych, pooddzielanych
pojedynczymi odstępami:
różnych liczb całkowitych, pooddzielanych
pojedynczymi odstępami: 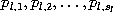 - numery kolejnych przystanków na tej linii
(
- numery kolejnych przystanków na tej linii
(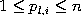 , dla
, dla 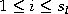 ).
).
-
W trzecim wierszu opisującym linię komunikacyjną
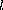 jest
zapisanych
jest
zapisanych 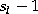 liczb całkowitych, pooddzielanych
pojedynczymi odstępami:
liczb całkowitych, pooddzielanych
pojedynczymi odstępami: 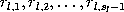 - czasy przejazdów (w minutach) pomiędzy kolejnymi
przystankami na tej linii
(
- czasy przejazdów (w minutach) pomiędzy kolejnymi
przystankami na tej linii
(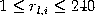 ,
dla
,
dla 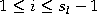 ).
).
Suma liczb przystanków, na wszystkich liniach razem, nie przekracza 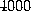 (tzn.
(tzn. 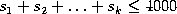 ).
).
Wyjście
Twój program powinien zapisać w pierwszym i jedynym wierszu
standardowego wyjścia dwie liczby całkowite oddzielone
pojedynczym odstępem: godzinę dotarcia do przystanku końcowego
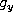 (
(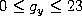 ) oraz minutę dotarcia do przystanku końcowego
) oraz minutę dotarcia do przystanku końcowego
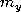 (
(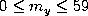 ).
).
Przykład
Dla danych wejściowych:
6 2 5 6 23 30 4 15 1 3 4 6 9 12 10 4 20 5 3 4 2 11 17 11
poprawną odpowiedzią jest:
0 16
Autor zadania: Zbigniew J. Czech.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English